
| 位或运算符: 这个运算符用于对两个二进制数字的对应位执行或操作,只要两个数字的对应位中至少有一个是 1,结果位就是 1。
const a = 5; // 二进制: 101
const b = 3; // 二进制: 011
const result = a | b; // 位或操作
console.log(result); // 输出: 7 (二进制: 111)& 位与运算符: 这个运算符用于对两个二进制数字的对应位执行与操作,只有在两个数字的对应位都是 1 时,结果位才是 1,否则为 0。
const a = 5; // 二进制: 101
const b = 3; // 二进制: 011
const result = a & b; // 位与操作
console.log(result); // 输出: 1 (二进制: 001)奇数 & 1 返回1 ,Number & 1 === 1
^ 位异或运算符: 这个运算符用于对两个二进制数字的对应位执行异或操作,只有在两个数字的对应位不相同时,结果位才是 1,否则为 0。
const a = 5; // 二进制: 101
const b = 3; // 二进制: 011
const result = a ^ b; // 位异或操作
console.log(result); // 输出: 6 (二进制: 110)~ 位非运算符: 这个运算符用于对一个二进制数字的每一位执行非操作,将 0 变为 1,将 1 变为 0。
const a = 5; // 二进制: 101
const result = ~a; // 位非操作
console.log(result); // 输出: -6 (二进制: 11111111111111111111111111111010,注意这是有符号整数表示)~(1) = -2
~(2) = -3
>> 右移运算符 << 左移运算符: 这个运算符将一个二进制数字向右移动指定的位数,丢弃最右边的位,同时在最左边添加相同数量的符号位(正数为 0,负数为 1),以保持符号不变。
const a = 16; // 二进制: 10000
const result = a >> 2; // 右移 2 位
console.log(result); // 输出: 4 (二进制: 0010)
应用场景
可以在rgb颜色和16进制颜色之间转换
原码
是最简单的机器数表示法,用最高位表示符号位,其他位存放该数的二进制的绝对值
以带符号位的四位二进制数为例:1010,最高位为1表示这是一个负数,其它三位010,即02^2+12^1+0*2^0=2,所以1010表示十进制数-2。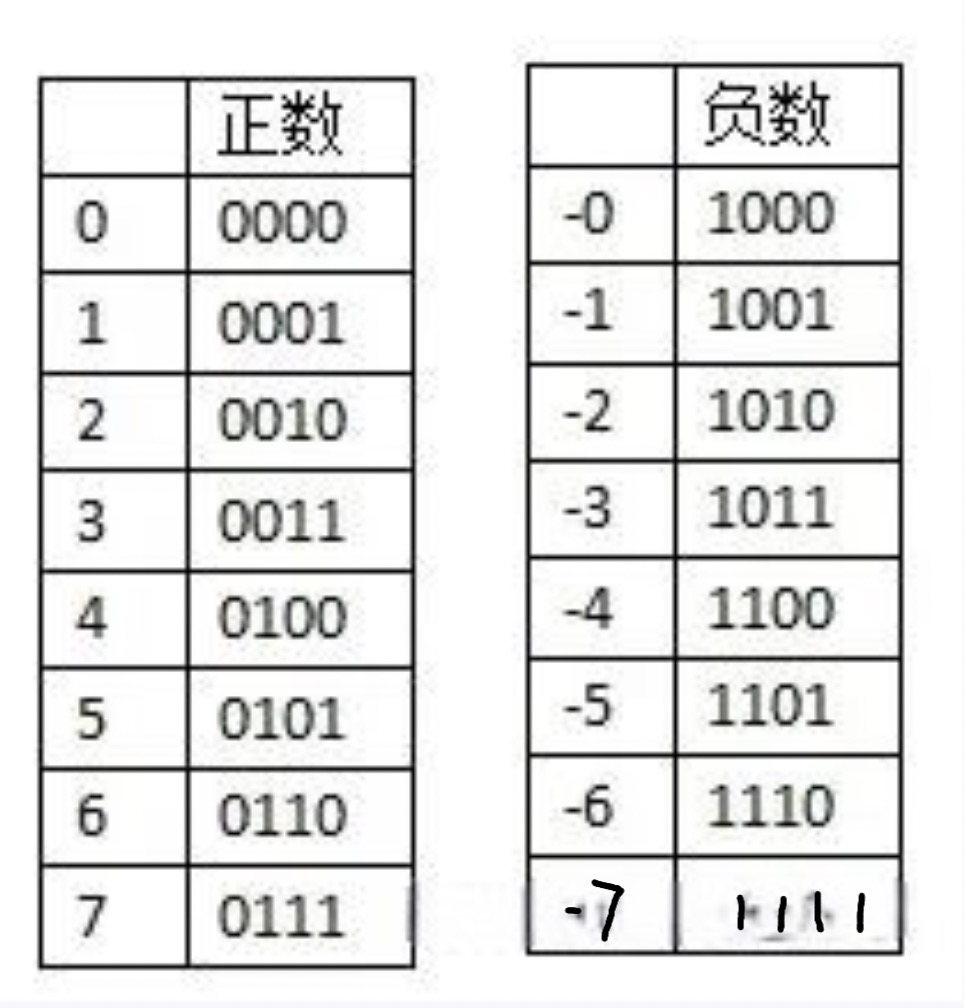
原码的表示法很简单,虽然出现了+0和-0,但是直观易懂。于是开始运算——
于是可以看到其实正数之间的加法通常是不会出错的,因为它就是一个很简单的二进制加法,而正数与负数相加,或负数与负数相加,就要引起莫名其妙的结果,这都是符号位引起的。0分为+0和-0也是因它而起。
原码的特点:
- 原码表示直观、易懂,与真值转换容易。
- 原码中0有两种不同的表示形式,给使用带来了不便。
原码表示加减运算复杂。
反码
正数的反码还是等于原码;负数的反码就是它的原码除符号位外,按位取反。
原码最大的问题就在于一个数加上它的相反数不等于0,于是反码的设计思想就是冲着解决这一点,既然一个负数是一个正数的相反数,那干脆用一个正数按位取反来表示负数。
以带符号位的四位二进制数为例:3是正数,反码与原码相同,则可以表示为0011;-3的原码是1011,符号位保持不变,低三位按位取反,所以-3的反码为1100。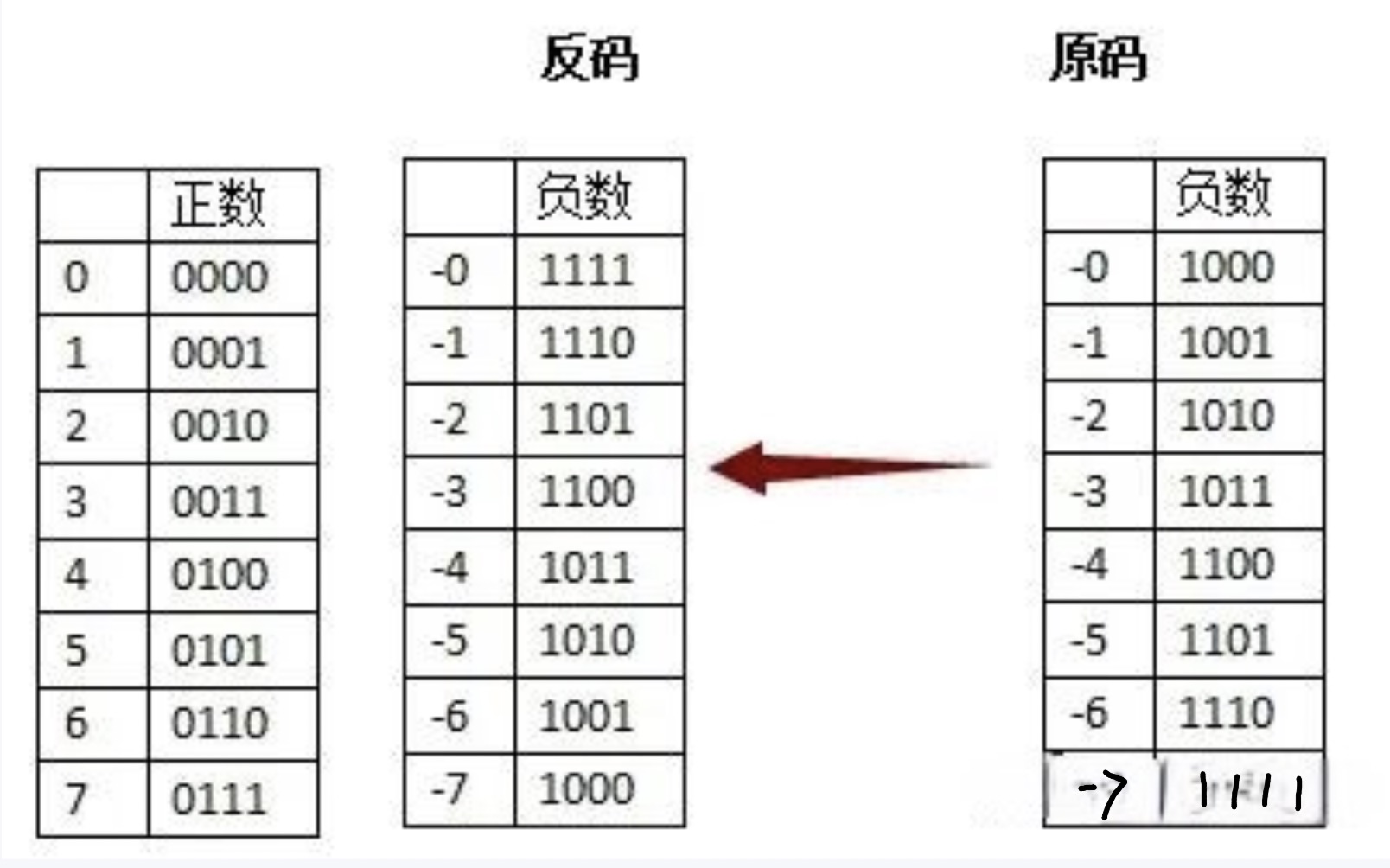
再试着用反码的方式解决一下原码的问题——
互为相反数相加等于0,虽然的到的结果是1111也就是-0。但是两个负数相加的出错了。
反码的特点:
- 在反码表示中,用符号位表示数值的正负,形式与原码表示相同,即0为正;1为负。
- 在反码表示中,数值0有两种表示方法。
反码的表示范围与原码的表示范围相同。
反码表示在计算机中往往作为数码变换的中间环节。
补码
正数的补码等于它的原码;负数的补码等于反码+1(这只是一种算补码的方式,多数书对于补码就是这句话)。
其实负数的补码等于反码+1只是补码的求法,而不是补码的定义,很多人以为求补码就要先求反码,其实并不是,那些计算机学家并不会心血来潮的把反码+1就定义为补码,只不过补码正好就等于反码+1而已。
如果有兴趣了解补码的严格说法,建议可以看一下《计算机组成原理》,它会用“模”和“同余”的概念,严谨地解释补码。
补码的思想
补码的思想,第一次见可能会觉得很绕,但是如果肯停下来仔细想想,绝对会觉得非常美妙。
补码的思想其实就是来自于生活,只是我们没注意到而已,如时钟、经纬度、《易经》里的八卦等。 补码的思想其实就类似于生活中的时钟。
如果说现在时针现在停在10点钟,那么什么时候会停在八点钟呢?
所以12在时钟运算中,称之为模,超过了12就会重新从1开始算了。
也就是说,10-2和10+10从另一个角度来看是等效的,它都使时针指向了八点钟。
既然是等效的,那么在时钟运算中,减去一个数,其实就相当于加上另外一个数(这个数与减数相加正好等于12,也称为同余数),这就是补码所谓运算思想的生活例子。
在这里,再次强调原码、反码、补码的引入是为了解决做减法的问题。在原码、反码表示法中,我们把减法化为加法的思维是减去一个数等于加上这个数的相反数,结果发现引入符号位,却因为符号位造成了各种意想不到的问题。
但是从上面的例子中,可以看到其实减去一个数,对于数值有限制、有溢出的运算(模运算)来说,其实也相当于加上这个数的同余数。
也就是说,不引入负数的概念,就可以把减法当成加法来算。
补码的实例
接下来就做一做四位二进制数的减法(先不引入符号位)。
0110-0010,6-2=4,但是由于计算机中没有减法器,没法算。
这时候,想想时钟运算中,减去一个数,是可以等同于加上另外一个正数(同余数),这个数与减数相加正好等于模。
也就是四位二进制数最大容量是多少?其实就是2^4=16(10000)。
那么-2的同余数,就等于10000-0010=1110,16-2=14。
既然如此,0110-0010=0110+1110=10100,6-2=6+14=20。
按照这种算法得出的结果是10100,但是对于四位二进制数最大只能存放4位,如果低四位正好是0100,正好是想要的结果,至于最高位的1,计算机会把它放入psw寄存器进位位中,8位机会放在cy中,x86会放在cf中,这里不做讨论。
这个时候,再想想在四位二进制数中,减去2就相当于加上它的同余数(至于它们为什么同余,还是建议看《计算机组成原理》)。
但是减去2,从另一个角度来说,也是加上-2,即加上-2和加上14得到的二进制结果除了进位位,结果是一样的。如果我们把1110的最高位看作符号位后就是-2的补码,这可能也是为什么负数的符号位是1,而不是0。
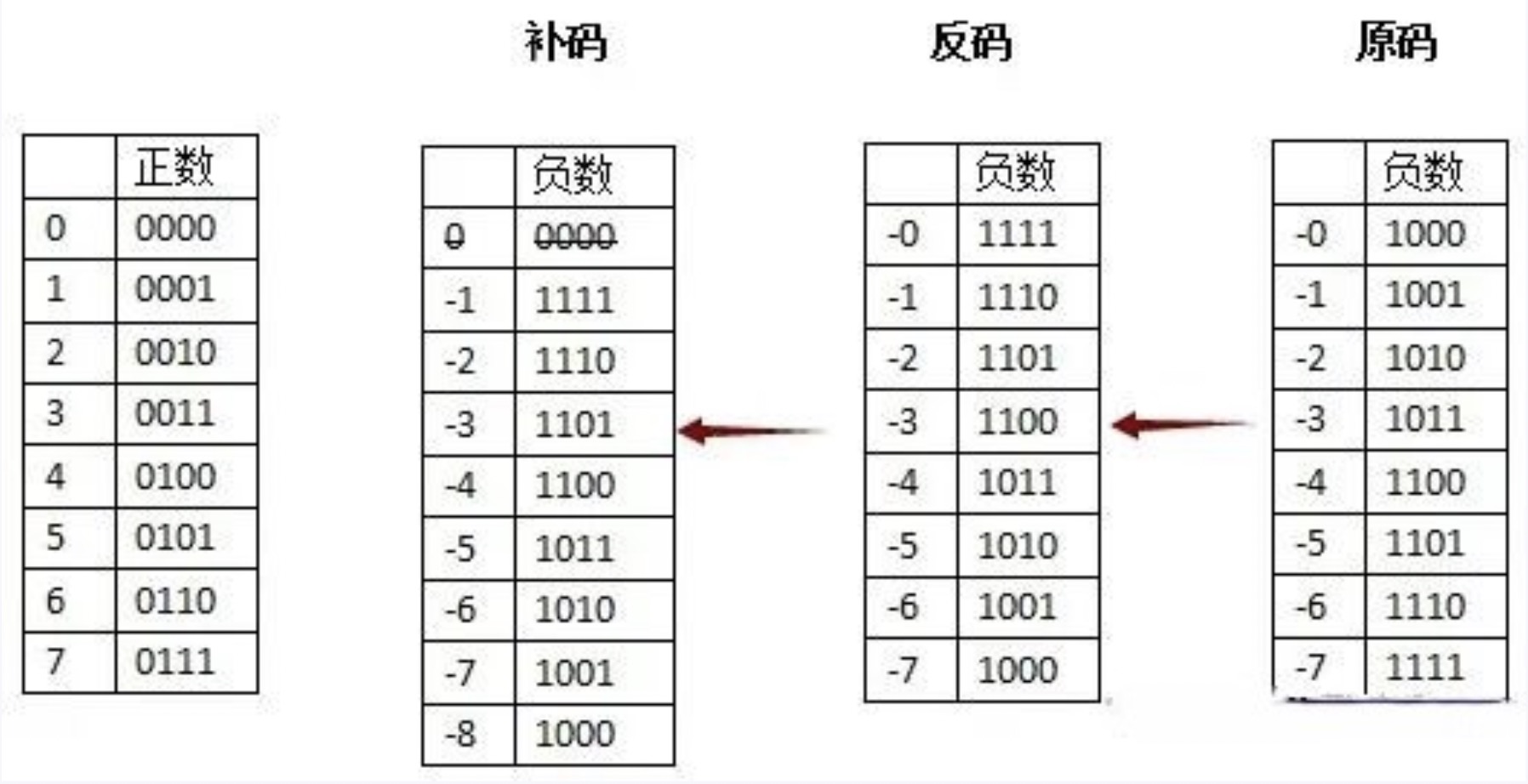
到这里,原码、反码的问题,补码基本解决了。
在补码中也不存在-0了,因为1000表示-8。
补码的特点:
在补码表示中,用符号位表示数值的正负,形式与原码的表示相同,即0为正,1为负。但补码的符号可以看做是数值的一部分参加运算。
- 在补码表示中,数值0只有一种表示方法。
- 负数补码的表示范围比负数原码的表示范围略宽。纯小数的补码可以表示到-1,纯整数的补码可以表示到-2^n。
由于补码表示中的符号位可以与数值位一起参加运算,并且可以将减法转换为加法进行运算,简化了运算过程, 因此计算机中均采用补码进行加减运算。
为什么负数的补码的求法是反码+1
拿-2举例:
【正整数2的原码】 (0010)
【正整数2的反码】(1101)
【-2的原码】 (1010)
【-2的反码】 (1101)
【-2的补码】 (1110)
【-2的绝对值】=【正整数2的原码】 (0010)
因为负数的反码(1101)加上这个负数的绝对值(0010)正好等于1111(1101+0010=1111),在加1,就是10000,也就是四位二进数的模,而负数的补码(1110)是它的绝对值(0010)的同余数(10000-0010=1110),可以通过模减去负数的绝对值(10000-0010=1110)得到它的补码(1110),所以负数的补码就是它的反码+1(1101+1=1110)。 【-2的补码】 + 【-2的绝对值】 = 【-2的反码】 + 【-2的绝对值】 + 1 = 模(10000) -> 【-2的补码】 = 【-2的反码】 + 1
文章来源,感谢原作者的无私分享:
https://zhuanlan.zhihu.com/p/99082236
https://juejin.cn/post/6967233795623747614
https://www.php.cn/faq/489781.html


评论 (0)